지난 포스팅에서 연결 리스트를 활용해 다양한 데이터 구조를 만들어봤습니다. 연결 리스트는 각 요소가 다른 요소를 하나씩만 가리키고 있었는데 만약 가리키는 요소가 더 많아진다면 어떻게 될까요? 오늘은 연결 리스트 기반의 자료구조인 '트리'에 대해 공부해보도록 하겠습니다.
트리는 기존 연결리스트의 각 노드들의 연결과 달리 2차원적으로 구성되어있는 연결입니다. 각 노드는 일정한 층에 속하게 되고, 다음 층의 노드들을 가리키는 포인터를 갖게 됩니다.
쉽게 그림으로 표현하자면

이렇게 기존 연결 리스트의 각 노드들이 1차원적으로 연결되어 있었다면
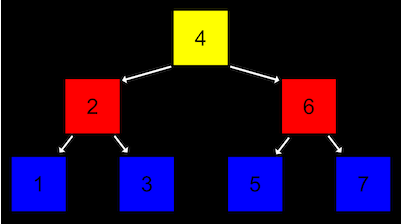
트리는 이렇게 표현합니다.
여기서 가장 높은 층에서 트리가 시작되는 노드를 '루트'라고 합니다. 루트 노드는 다음 층의 노드들을 각각 가리키고 있고 이를 '자식 노드'라고 합니다.
위 트리구조의 그림은 이진 검색 트리인 것을 알 수 있습니다.
왜 그런가 하면 하나의 노드가 2개의 자식 노드를 가지고 자신을 기준으로 왼쪽 자식 노드는 자신보다 값이 작고, 오른쪽 자식 노드는 자신보다 값이 큰 것을 알 수 있습니다.
이렇게 표현하게 되면 기존 연결 리스트보다 검색시간이 훨씬 빠르게 되겠죠 하지만 위 그림처럼 좌우 균형이 맞지 않게 될 경우(즉 한쪽이 길어지거나 할 경우) 조건에 따라서 기존 연결 리스트와 큰 차이가 없게 될 수도 있습니다.
그러면 트리구조를 코드로 바꿔 50을 재귀적으로 검색하는 이진 검색 함수를 표현하면 어떨까요?
typedef struct node
{
int number;
struct node *left;
struct node *right;
}
node;
// 이진 검색 함수
bool search(node *tree)
{
// 트리가 비어있는 경우 false
if (tree == NULL)
{
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number)
{
return search(tree->left);
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number)
{
return search(tree->right);
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 true
else {
return true;
}
}이런 식으로 표현할 수 있습니다.
이때 검색 실행시간과 노드 삽입 시간을 표현하면 O(log n)이 됩니다.
출처
본 내용은 CS50의 2019년 강의를 듣고 작성했습니다. (개념이 어느 정도 정리되면 최신강의도 다시 듣고 수정할 내용 있으면 수정하겠습니다.)
강의 자료는 EdX에서 무료로 사용할 수 있고 boostcourse에서 한글 강의로도 들을 수 있습니다.
'CS 기초 > 자료구조' 카테고리의 다른 글
| [CS50] 스택, 큐, 딕셔너리 (0) | 2021.09.04 |
|---|---|
| [CS50] 트라이 (0) | 2021.09.03 |
| [CS50] 연결리스트 : 시연 (0) | 2021.08.31 |
| [CS50] 연결리스트 : 코딩 (0) | 2021.08.30 |
| [CS50] 연결리스트 : 도입 (0) | 2021.08.29 |